(1) 기수법(numeral system)이란
‘기수법’이란, 기호(symbol)를 이용해 수1를 표현하는 체계적인 방법을 말한다. 가장 단순한 기수법에는 1에 해당하는 수를 ‘/’와 같은 기호로 표기하고, 1보다 큰 수에 대해서는 기호 ‘/’의 개수로 나타내는 ‘단항기수법(unary numeral system)’이 있다.
일상생활에서 단항기수법은 수를 보다 읽기 쉽도록 위치와 모양을 변형해 다섯 개의 ‘/’을 하나의 기호처럼 보이도록 한다. 아래의 그림과 같은 것인데 이는 학급임원 선거 때 한 번쯤 써보았을 것이다.

단항기수법의 원리상 기호 ‘/’의 위치는 전혀 고려되지 않는데 이러한 성질을 가진 기수법을 ‘비(非)자릿수 기수법’이라 한다.
반면, 기호를 나열하여 수를 나타내되 위치에 따라 기호가 나타내는 값이 달라지는 기수법을 ‘자릿수 기수법’ 또는 ‘위치 기수법’이라 한다. 특히, 0, 1, 2, …, p-1이라는 p개의 숫자만을 조합하여 사용하는 자릿수 기수법을 ‘p진법(p-base system)“이라고 한다. p진법은 자리의 위치에 따라 오른쪽에서부터 1, p, p^2, p^3, …으로 자릿수가 p배로 커지는 기수법이다.
우리가 사용하는 자연수의 진법은 p=10인 ’10진법(decimal system)’이다. 10진법은 0부터 9까지 10개의 숫자를 사용하고, 오른쪽에서부터 1, 10, 10^2, 10^3, …으로 자릿수가 10배로 커진다. 예를 들면 숫자 1을 3개 나열하여 만든 수 111에서 일의 자리에 있는 1은 그대로 1을 의미하지만, 십의 자리에 있는 1은 10을 의미하고, 백의 자리에 있는 1은 100을 의미한다.
일반적으로 p진법은 p의 값에 따라 2진법, 3진법, …이라 부르는데, 이들은 사용되는 숫자의 종류와 위치에 따른 자릿수가 10진법과 다를 뿐, 숫자의 나열 방식은 동일하므로 10진법과의 구분을 명확히 하기 위해 111(2), 111(5)와 같이 끝에 p의 값을 표기해 놓는다.
자연수 111과 111(2), 111(5)이 어떻게 다른지는 다음과 같이 자릿수의 비교로 충분히 알 수 있다.
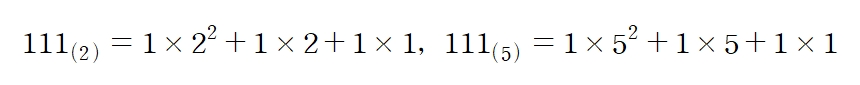
이때 위의 식과 같이 p진법으로 나타낸 수의 값을 p의 거듭제곱을 이용하여 식으로 표현한 것을 ‘p진법의 전개식’이라고 한다. 이 전개식을 계산하면 p진법의 수가 십진법으로 얼마와 같은지 알 수 있다.
· p진법의 전개식
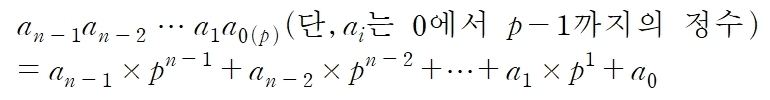
한편 p진법의 전개식으로부터 우리는 자연수의 나눗셈을 이용해 십진법의 수를 p진법으로 표현하는 방법을 터득할 수 있다.
아래는 십진법의 수 15를 이진법의 수로 변환하는 과정이다.

이를 아래와 같이 2의 나눗셈만으로 간단하게 구할 수 있다.

과정이 복잡해 보이지만 사실 기수법은 숫자 놀이에 불과하다. 자릿수 기수법에 대한 이해를 바탕으로 나눗셈의 몫과 나머지를 잘 구하면 된다.

(2) p진법의 전개식과 다항식의 관계
10진법의 전개식
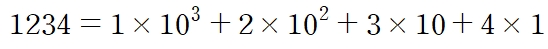
에서 10을 x로 바꾸면

이 되는데 언뜻 보기에는 다항식과 매우 유사하다. 수의 전개식과 다항식 사이에 보이는 묘한 공통점을 잘 이용하면 진법을 변환해야 할 때 다항식을 세운 다음 항등식의 성질을 이용하여 미정계수를 구할 수도 있다.
10진법의 수 7421을 7진법의 수로 나타내는 방법을 생각해 보자.
우리의 목표는 7421의 10진법의 전개식을 7진법의 전개식으로 변환하는 것이므로, 다음 수식에서 우변의 계수를 구하는 것이 목적이다.
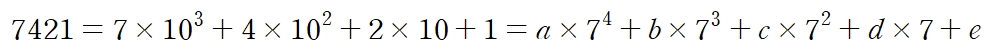
여기서 7^4=2401이기 때문에, 7421을 7진법으로 바꾸면 5자리의 수가 되고, a, b, c, d, e는 0부터 6까지의 정수이다. 위 식에서 진수를 의미하는 10과 7을 각각 x, x-3이라고 하면
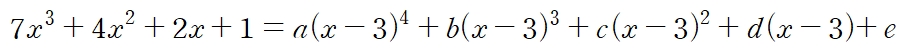
가 된다. 어디선가 많이 본 모양이지 않은가? 위의 형태는 조립제법에서 이미 접했었다. 다만, 우리가 배웠던 조립제법은 나머지가 ‘0부터 6까지의 정수’라는 조건을 고려하지 않은 것이므로, a, b, c, d, e를 결정하기 위해서는 약간의 기술적인 변형을 필요로 한다.

위의 과정을 수식으로 쓰면 다음과 같다. 밑줄 친 부분은 조립제법의 한 부분이다.
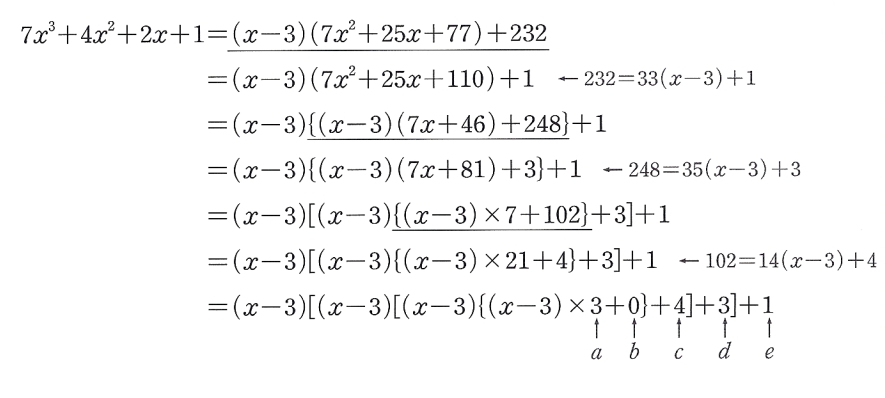
- 발췌 및 수정 : 《숨마쿰라우데》

- 엄밀히 따져서 숫자(digit)와 수(number)는 다르다. 숫자는 수를 ‘글자’로 나타낸 것을 말하며, 수는 세거나 측정하여 느낄 수 있는, 이를 통해 머리에서 떠올릴 수 있는 추상적인 대상이다. [본문으로]
'정신체조수학' 카테고리의 다른 글
| 대수학의 기본 정리 (0) | 2022.12.23 |
|---|---|
| 이차방정식의 근과 복소수의 탄생 (1) | 2022.12.19 |
| 어떻게 나눌까? (2) | 2021.11.12 |
| 2015 개정 고등수학 교육과정 (2) | 2017.10.13 |





댓글